Before you get started, take this readiness quiz.
Remember that an exponent indicates repeated multiplication of the same quantity. For example, \(2^4\) means the product of \(4\) factors of \(2\), so \(2^4\) means \(2·2·2·2\).
Let’s review the vocabulary for expressions with exponents.
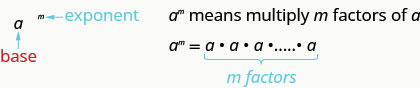times a times a times a, followed by an ellipsis, with “m factors” written below in blue." />
This is read \(a\) to the \(m^\) power.
In the expression \(a^\), the exponent \(m\) tells us how many times we use the base a as a factor.
written below in blue. The right column contains negative 9 to the fifth power. Below this is negative 9 times negative 9 times negative 9 times negative 9 times negative 9, with “5 factors” written below in blue." />
Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.
Solution
